变量之间存在着相关关系,比如,人的身高和体重之间存在着关系,一般来说,人高一些,体重要重一些,身高和体重之间存在的是不确定性的相关关系。回归分析是研究相关关系的一种数学工具,它能帮助我们从一个变量的取值区估计另一个变量的取值。
OLS(最小二乘法)主要用于线性回归的参数估计,它的思路很简单,就是求一些使得实际值和模型估值之差的平方和达到最小的值,将其作为参数估计值。就是说,通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
一,OLS回归
OLS法通过一系列的预测变量来预测响应变量(也可以说是在预测变量上回归响应变量)。线性回归是指对参数β为线性的一种回归(即参数只以一次方的形式出现)模型:
Yt=α+βxt+μt (t=1……n)表示观测数
- Yt 被称作因变量
- xt 被称作自变量
- α、β 为需要最小二乘法去确定的参数,或称回归系数
- μt 为随机误差项
OLS线性回归的基本原则:最优拟合曲线应该使各点到直线的距离的平方和(即残差平方和,简称RSS)最小:
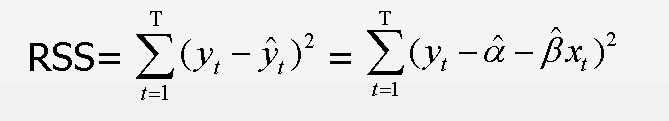
OLS线性回归的目标是通过减少响应变量的真实值与预测值的差值来获得模型参数(截距项和斜率),就是使RSS最小。
为了能够恰当地解释OLS模型的系数,数据必须满足以下统计假设:
- 正态性:对于固定的自变量值,因变量值成正太分布
- 独立性:个体之间相互独立
- 线性相关:因变量和自变量之间为线性相关
- 同方差性:因变量的方差不随自变量的水平不同而变化,即因变量的方差是不变的
二,用lm()拟合回归模型
在R中,拟合回归模型最基本的函数是lm(),格式为:
lm(formula, data)
formula中的符号注释:
- ~ 分割符号,左边为因变量,右边为自变量,例如, z~x+y,表示通过x和y来预测z
- + 分割预测变量
- : 表示预测变量的交互项,例如,z~x+y+x:y
- * 表示所有可能的交互项,例如,z~x*y 展开为 z~x+y+x:y
- ^ 表示交互项的次数,例如,z ~ (x+y)^2,展开为z~x+y+x:y
- . 表示包含除因变量之外的所有变量,例如,如果只有三个变量x,y和z,那么代码 z~. 展开为z~x+y+x:y
- -1 删除截距项,强制回归的直线通过原点
- I() 从算术的角度来解释括号中的表达式,例如,z~y+I(x^2) 表示的拟合公式是 z=a+by+cx2
- function 可以在表达式中应用数学函数,例如,log(z) ~x+y
对于拟合后的模型(lm函数返回的对象),可以应用下面的函数,得到模型的更多额外的信息。
- summary() 展示拟合模型的详细结果
- coefficients() 列出捏模型的参数(截距项intercept和斜率)
- confint() 提供模型参数的置信区间
- residuals() 列出拟合模型的残差值
- fitted() 列出拟合模型的预测值
- anova() 生成一个拟合模型的方差分析表
- predict() 用拟合模型对新的数据预测响应变量
例如,使用基础安装包中的数据集women(包含了年龄在30-39岁之间女性的身高和体重信息),通过身高来预测体重。
1,线性拟合
使用lm()函数来拟合模型,获得模型对象fit
fit <- lm(weight~height,data=women)
使用summary()函数来查看模型的信息:
> summary(fit)Call:lm(formula = weight ~ height, data = women)Residuals: Min 1Q Median 3Q Max -1.7333 -1.1333 -0.3833 0.7417 3.1167 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***height 3.45000 0.09114 37.85 1.09e-14 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 1.525 on 13 degrees of freedomMultiple R-squared: 0.991, Adjusted R-squared: 0.9903 F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
残差标准差(Residual standard error):表示模型用身高来预测体重的平均误差
R的平方项(Multiple R-squared):表明模型可以解释体重99.1%的方差,是实际和预测值之间相关系数的平方。
F统计量(F-statistic):检验所有的预测变量预测响应变量是否都在某个概率水平之上,
从Coefficients 组中,可以看到 Intercept(截距项)是 - 87.51667,height的系数是3.45,截距项和系数的标准差、t值和Pr(>|t|),其中,Pr(>|t|) 表示双边检验的p值
注,p值的表示方法通常有p-value,或Pr,p值是概率,表示某一事件发生的可能性大小。如果P值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,我们拒绝原假设的理由越充分。总之,P值越小,表明结果越显著。
因此可以得到预测等式:
Weight= - 87.51667 + 3.45 * Height
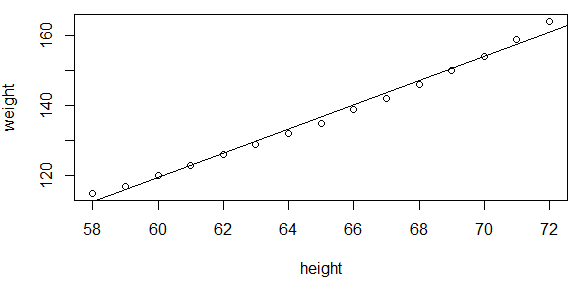
绘制拟合的直线:
> plot(women$height, women$weight,xlab='height',ylab='weight')> abline(fit)
2,多项式拟合
使用lm(),在formula参数中使用I()函数来进行多项式拟合
> fit2 <- lm(weight~I(height^2),data=women)> plot(women$height, women$weight,xlab='height',ylab='weight')> lines(women$height,fitted(fit2))> summary(fit2)Call:lm(formula = weight ~ I(height^2), data = women)Residuals: Min 1Q Median 3Q Max -1.2562 -0.7636 -0.1837 0.4622 2.2654 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.390e+01 2.109e+00 11.34 4.12e-08 ***I(height^2) 2.659e-02 4.926e-04 53.98 < 2e-16 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 1.072 on 13 degrees of freedomMultiple R-squared: 0.9956, Adjusted R-squared: 0.9952 F-statistic: 2913 on 1 and 13 DF, p-value: < 2.2e-16
非线性模型可用nls()函数进行拟合。
三,回归诊断(标准方法)
回归诊断用于评价回归模型的拟合程度,模型返回的参数多大程度上匹配原始数据。
根据OLS回归的统计假设来评价模型的拟合情况,对于lm()拟合的模型对象,使用plot()函数生成评价模型拟合情况的四幅图形,
> fit <- lm(weight~height,data=women)> par(mfrow=c(2,2))> plot(fit)
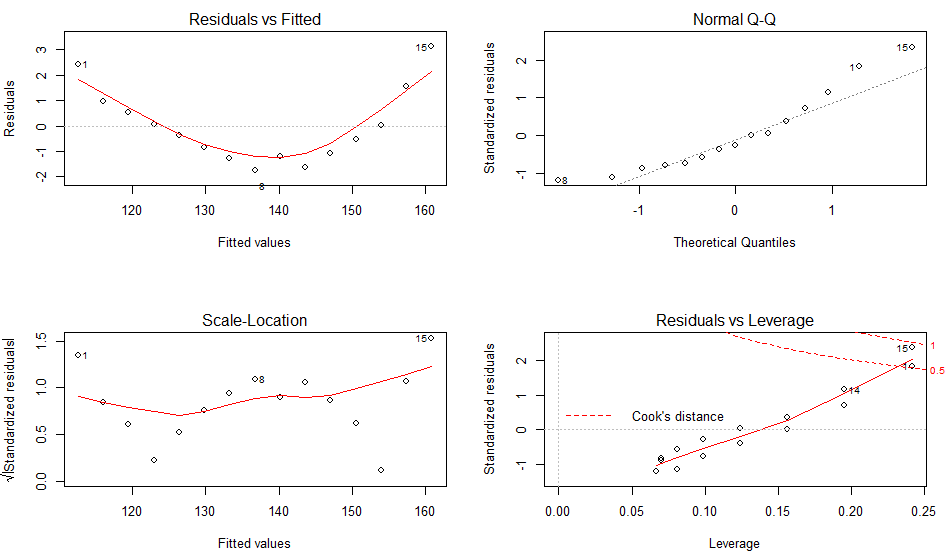
正态性:当预测变量值固定时,因变量成正态分布,则残差值也应该是一个均值为0的正态分布。正态QQ图(Normal Q-Q)是在正态分布对应的值下,标准化残差的概率图。若满足正态假设,那么图上的点应该落在呈45度角的直线上;若不是如此,那么久违反了正态假设。
独立性:无法判断因变量和自变量的值是否相互独立,只能从收集的数据中来验证。
线性相关性:若因变量与自变量线性相关,那么残差值与预测(拟合)值除了系统误差之外,就没有任何关联。在残差和拟合图(Residuals VS Fitted)中,可以看到一条曲线,这暗示着可能需要对拟合模型加上一个二次项。
同方差性:若满足不变方差假设,那么在位置尺度图(Scale-Location)中,水平线周围的点应该随机分布。
残差和杠杆图(Residuals VS Leverage)提供了特殊的单个观测点(离群点、高杠杆点、强影响点)的信息。
- 离群点:表明拟合回归模型对其预测效果不佳(产生巨大的残差)
- 高杠杆点:指自变量因子空间中的离群点(异常值),由许多异常的自变量值组合起来的,与因变量没有关系。
- 强影响点:表明它对模型参数的估计产生的影响过大,非常不成比例。强影响点可以通过Cook距离(Cook distance)统计量来前别。
残差和杠杆图的可读性差,不够实用。
什么是高杠杆点?离群点是指对于给定的预测值 ![]() 来说,响应值
来说,响应值 ![]() 异常的点。相反,高杠杆(high leverage) 表示观测点
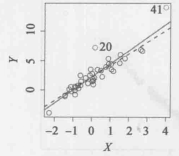
异常的点。相反,高杠杆(high leverage) 表示观测点 ![]() 是异常的。例如,图1(a)左下图中的观测点41具有高杠杆值,因为它的预测变量值比其他观测点都要大。实线是对数据的最小二乘拟合,而虚线是删除观测点41后的拟合。事实上,高杠杆的观测往往对回归直线的估计有很大的影响。如果一些观测对最小二乘线有重大影响,那么它们值得特别关注,这些点出现任何问题都可能使整个拟合失效。因此找出高杠杆观测是十分重要的 。
是异常的。例如,图1(a)左下图中的观测点41具有高杠杆值,因为它的预测变量值比其他观测点都要大。实线是对数据的最小二乘拟合,而虚线是删除观测点41后的拟合。事实上,高杠杆的观测往往对回归直线的估计有很大的影响。如果一些观测对最小二乘线有重大影响,那么它们值得特别关注,这些点出现任何问题都可能使整个拟合失效。因此找出高杠杆观测是十分重要的 。
四,回归诊断(car包)
car包提供了大量的函数,大大增强了拟合和评价回归模型的能力
1,正态性
qqplot()函数提供了精确的正态假设检验方法,
> library(carData)> library(car)> par(mfrow=c(1,2))> fit <- lm(weight~height,data=women)> qqPlot(fit,labels=row.names(women),id.method='identity',simulate=TRUE,main='qq-fit')[1] 1 15> fit2 <- lm(weight~height+I(height^2),data=women)> qqPlot(fit2,labels=row.names(women),id.method='identity',simulate=TRUE,main='qq-fit2')[1] 13 15
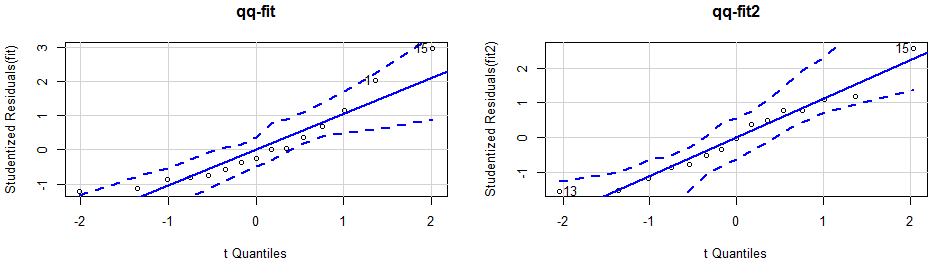
可以看到,置信区间通过虚线划定,当绝大多数点都落在置信区间时,说明正态性假设符合的很好。
2,误差的独立性
car包提供了durbinWatsonTest()函数,用于做Durbin-Watson检验,检测误差的序列相关性。
> durbinWatsonTest(fit) lag Autocorrelation D-W Statistic p-value 1 0.585079 0.3153804 0 Alternative hypothesis: rho != 0
p值 (p=0)不显著,误差项之间独立
3,线性相关性
通过成分残差图(component + residual plots)检查因变量和自变量之间是否呈线性关系。
crPlots(fit)
若图形存在非线性,则说明可能对预测变量的函数形式建模不够充分,那么需要添加一些曲线成分,比如多项式,对一个或多个变量进行变换(log(x)代替x),或用其他回归变体形式而不是线性回归。
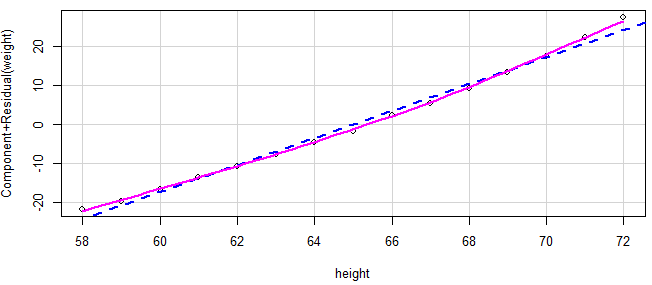
4,同方差性
判断方差是否恒定,nvcTest()函数生成一个记分检验,原假设为误方差不变,备择假设为误差方差随着拟合值水平的变化而变化。若检验显著,说明存在误方差不很定。
spreadLevelPlot()函数创建了一个添加了最佳拟合曲线的散点图,展示了标准化残差绝对值与拟合值得关系。
> ncvTest(fit)Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 0.8052115, Df = 1, p = 0.36954> spreadLevelPlot(fit)Suggested power transformation: -0.8985826
记分检验不显著:p=0.36954,说明满足方差不变假设,也可以通过分布水平看到这一点,点在水平的最佳拟合曲线周围呈随机分布。

五,回归诊断(gvlma包)
gvlma()函数,用于对线性模型假设进行综合验证,同事还能验证偏斜度,峰度和异方差的评价。从输出项中可以看出,假设检验的显著性水平是5%。如果p<0.05,说明违反了假设条件。从Global Stat 的Decision 栏中,可以看到数据满足OLS回归模型所有的统计假设(p=0.597)。
> library(gvlma)> gvmodel <- gvlma(fit)> summary(gvmodel).................ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONSUSING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:Level of Significance = 0.05 Call: gvlma(x = fit) Value p-value DecisionGlobal Stat 16.5866 0.0023251 Assumptions NOT satisfied!Skewness 1.5577 0.2119999 Assumptions acceptable.Kurtosis 0.1019 0.7496131 Assumptions acceptable.Link Function 14.1218 0.0001713 Assumptions NOT satisfied!Heteroscedasticity 0.8052 0.3695398 Assumptions acceptable.
参考文档: